|
|
American Association of Physics Teachers |
|
|
Rai
Weiss's TALK
-- p. 6 About Teaching General Relativity: History, motivation, experiment from the AAPT Topical Workshop: Teaching General Relativity to Undergraduates Syracuse University, July 20-21, 2006 |
|
The 38 slides from Weiss's talk are here in 9 web pages. In the narrative below you can click on any subject to go to its page. Click here for a full PDF version. pg. 1 GR is one of several possible covariant theories of gravity. It is only from observation and experiment that we conclude that GR is the valid theory. So, Weiss argues, we should base the teaching of GR on experiment and observation. To make his points, he uses the historically important examples of gravitational red shift, bending of light, advance of perihelion of Mercury, Shapiro test, and Nordstrom's scalar theory of gravity, which, though Lorentz covariant, fails to predict correctly the precession of perihelion of Mercury or the gravitational redshift. pg. 2 You can motivate the need for curved space by imagining coordinates on a rotating platform. Basic phenomena, such as gravitational redshift, can be inferred from the principle of equivalence. The difficulty comes when you try to measure something: For the redshift there are subtle corrections to be determined and made. pg. 3 For bending of starlight around the Sun the effect is small and the results are ambiguous. pg. 4 Data from 9 solar eclipses show how imprecise these measurements were. There are no error bars, but tiny changes in the position or orientation of the plates or small shifts in the telescope from thermal variations occurring as the Sun was eclipsed would have produced large fractional errors in the results. There were other difficulties too. pg. 5 The modern data are much more precise and convincing. With radio interferometry the Sun's bending of microwaves from three radio stars has been measured to a precision of about 1%. pg. 6 Weiss contrasts the rate of precession of Mercury's perihelion with that of the apsides of the Hulse Taylor binary pulsar. Where the old measurements were only weak evidence for GR, modern measurements with precisions of ppm are strong evidence that GR is right. These data also yield convincing evidence for gravitational radiation as well as precise masses of the pulsar and its companion. Thirty years of observation continue to improve precision. pg. 7
Shapiro time delay
provides a good context for teaching about coordinate freedom. To test
two different theories you must make complete consistent calculations
with each. Shapiro had to express the results in coordinate free form
(as invariants), and then compare. He found that Einstein's GR predicted
what was observed; Newton's theory did not. pg. 8 Shortly after publishing his GR theory, Einstein showed that there should be gravitational radiation. To remind us that there are important subtleties in this prediction Weiss points out two mistakes that Einstein made in his first papers on gravity waves: 1) He erroneously predicted gravitational radiation from spherically symmetric motion, which we now understand to be impossible; 2) He made a factor of 2 error when calculated the quadrupolar radiation that is the dominant form of gravitational radiation. pg. 9 The take-home message: In the effort to detect gravitational radiation there is much other physics than gravity itself. Use it to interest your students. And motivate them with the elegance of the technical prowess and instruments needed to examine the physical consequences of GR. |
The table below shows the elaborate analysis needed to show that
GR is needed to account for 42.56 arc sec per century of precession of the
perihelion of
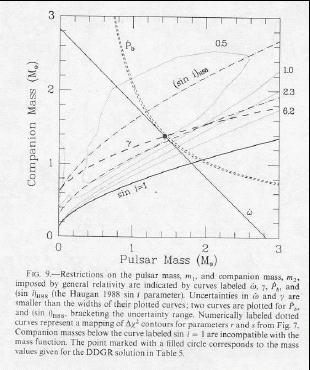
Mercury 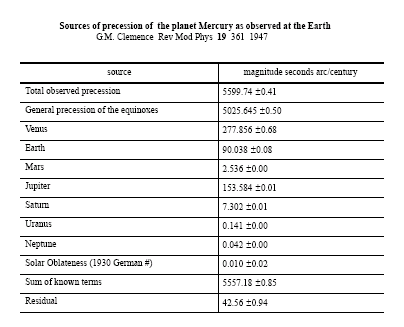 The Hulse Taylor binary pulsar 1913+16, on the other hand, exhibits a GR induced precession rate of 4.2 deg per year. Within 14 years many of its parameters have been measured with precisions of parts per million. 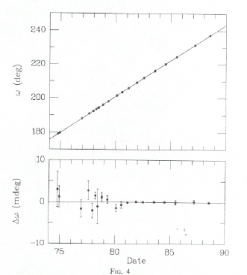
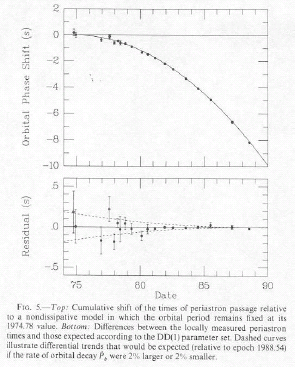
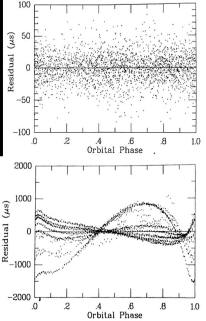 The above graph on the left shows the measured advance of the apsides of 1913+16 over 14 years. The line is the GR prediction. The upper graph at the right shows the residuals between the measured period and the predictions of GR. The bottom graph on the right shows the residuals when the GR corrections are omitted. Notice that the scales of the two graphs differ by a factor of 20. Clearly GR is needed to account for these observations. Data from 1913+16 also provided the first clear evidence of gravitational radiation. The graph below shows the cumulative shift of the times of periastron passage of the pulsar vs. time. The solid line is the slow-down that GR predicts will occur because of gravitational radiation. This is the first convincing evidence that there is gravitational radiation.
|